Welcome to another insightful piece presented to you by the FreeAstroScience.com team. Today, we delve deep into the fascinating world of astrophysics, exploring a phenomenon known as Hawking Radiation. This theory, proposed by the esteemed physicist Stephen Hawking in 1974, describes the black-body radiation emitted by black holes due to quantum effects near the event horizon. Let's unravel the intriguing details of Hawking Radiation and its implications on our understanding of black holes.
The Phenomenon of Hawking Radiation: An Overview
Hawking Radiation, named in honor of physicist Stephen Hawking who theorized its existence in 1974, is a form of black-body radiation predicted to emanate from black holes. This prediction is a consequence of quantum effects occurring close to the black hole's event horizon.
The Unruh Effect and The Principle of Equivalence
The existence of Hawking Radiation is necessitated by the principles of the Unruh effect and the equivalence principle as they apply to black hole horizons. An observer in the vicinity of a black hole's event horizon must accelerate to avoid being sucked in.
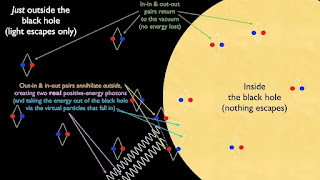
The Emission of Hawking Radiation
The accelerating observer perceives a thermal bath of particles that momentarily emerge from the local acceleration horizon, only to return by free-falling back into it. The presence of local thermal equilibrium suggests that this thermal bath, when consistently extended, has a finite temperature at infinity. This indicates that some particles released by the horizon won't be reabsorbed, thus becoming outgoing Hawking Radiation.
The Evaporation of Black Holes
When particles escape as Hawking Radiation, the black hole loses a fraction of its energy, and consequently, its mass. This process, known as black hole evaporation, implies that a black hole has a finite lifespan. The lifespan of a black hole can be determined to scale as the cube of its initial mass. Hawking estimated that any black hole formed in the early universe with a mass less than about 1015 g would have completely evaporated by now.
Quantum Effects and the Black Hole
The notion that black holes can "evaporate" and the radiated spectrum both emerge from an analysis of black hole thermal equilibrium. This is combined with extreme redshifting effects near the event horizon, and some consideration of quantum entanglement effects.
The Role of Photons
Near the event horizon, a pair of virtual waves or particles materialize due to quantum effects. These particles, which are almost always a pair of photons, can either pass beyond the event horizon or escape into the wider universe. The escaping photon is almost torn apart due to the exponential red-shifting effect of extreme gravity near the event horizon but is slightly amplified. The amplified photon gives rise to a "partner wave" carrying negative energy, which reduces the total energy of the black hole once it is trapped beyond the event horizon.
Conservation Law and Black Hole Evaporation
Despite this, no matter or energy ever exits the black hole itself. A conservation law exists for the partner wave, demonstrating that the emissions create an exact black body spectrum, revealing no information about the black hole's interior conditions.
Implications of Hawking Radiation
Hawking Radiation, also known as black hole evaporation, diminishes the mass and rotational energy of black holes. Hence, black holes not gaining mass through other means are predicted to shrink and eventually disappear, although this process would happen extremely slowly for all but the smallest black holes.
The Role of Micro Black Holes
The radiation temperature is inversely proportional to the black hole's mass, meaning micro black holes are predicted to emit more radiation than their larger counterparts and should thus shrink and dissipate faster. This insightful exploration into the world of black holes and Hawking Radiation sheds light on the incredible phenomena that govern our universe, brought to you by the dedicated team at FreeAstroScience.com.


Post a Comment