Football is a wonderful game that contains a lot of athleticism and physics. This is easily seen during a game where all the action unfolds. The main part of the physics of football involves the action of the ball and the players. This post will focus on describing and understanding some of the physics of both.
Football Flight
It is often the case that when a football is kicked or thrown, it undergoes an orientation change, when airborne, in which its long axis closely aligns with the flight path as it flies through the air. This orientation change is due to the effects of airflow over the football during flight. This orientation change happens when the football is given sufficient initial spin about its long axis. This creates gyroscopic stability which enables the football to keep its symmetric (long) axis aligned with its flight trajectory, without tumbling end over end when in flight. The spin imparts a gyroscopic response to the aerodynamic forces acting on the football, which results in the football long axis closely aligning itself with the flight trajectory (as shown below). The physics necessary to describe this is a combination of gyroscopic analysis and aerodynamic force analysis due to drag and (potentially) the Magnus effect. This is quite complicated and will not be discussed in detail here. However, there is a lot of literature available online on gyroscope physics, as related to projectile spin and gyroscopic stability, if one wishes to study this topic further.
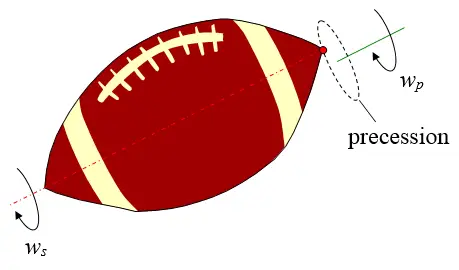
The reason the long axis of the football follows the flight path is because of the gyroscopic effect. When the football is kicked or thrown, it is given an initial spin along its long axis. Let's call this spin rate ws. Once the football is released and is airborne, it immediately reacts to the air flow past its surface, and this results in a secondary spin, referred to as precession. Let's call this precession rate wp. It is this precession that gives the football the appearance of "wobbling" during flight. The figure below illustrates the spin and precession of a football.
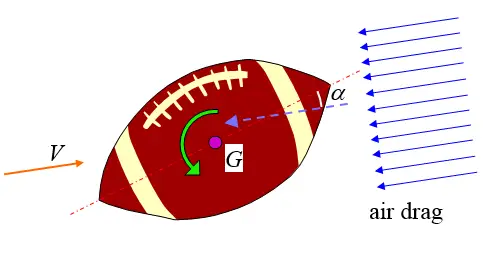
As the football flies through the air, the trajectory of its center of mass follows a curved path. In order to keep air resistance as low as possible, and maximize distance, it is desirable that the long axis of the football follows this path (as described previously). The force of the air (drag force) acting on the football serves to rotate the football such that the long axis closely aligns with the flight path. Consider the figure below which shows the football moving at an arbitrary velocity V during its flight through the air. The resultant air drag force (represented by the dashed arrow) is directly opposite the direction of V. If the long axis of the football is oriented at an angle α relative to the direction of the air drag, as shown, then the air drag force has a moment arm relative to the center of mass G of the football, and as a result the air drag force exerts a torque on the football (represented by the green arrow). This torque tends to increase α. However, α does not increase continuously, as one might expect. Instead, the long axis of the football follows closely with the flight path, due to a gyroscopic effect. When this occurs, the football precesses about an axis closely aligned with the line of the flight path, and this line is continuously changing direction, which means that the precession axis changes too. It can then be said that the long axis of the football closely follows the flight path. This means that the precession axis (which is in the direction of vector wp) is kept closely aligned with the flight path at any point in time. Keep in mind that this is an ideal circumstance, however, and football flight can sometimes deviate from this scenario.
Now, if this same football were launched in a vacuum (with no air present), with the same initial spin about its long axis, it would not change orientation at all, and instead it would maintain its orientation throughout its flight. The figure below illustrates this.
The reason the football doesn't change its orientation is because there is only the force of gravity which exerts no torque on the football since it effectively acts through the center of mass of the football.
For more detail on the physics behind the flight of a football see:
P. J. Brancazio, Why does a football keep its axis pointing along its trajectory?, The Physics Teacher, 23, 571-573 (1985).
C. Horn and H. Fearn, On the Flight of the American Football, Physics Department, California State University Fullerton (2007).
Interception
The diagram below shows a common situation in which a defender needs to intercept a receiver. In this situation, the travel path of the player doing the intercepting (the defender) must intersect the travel path of the receiver. The blue arrow represents the path of the receiver, and the green arrow represents the path of the defender.
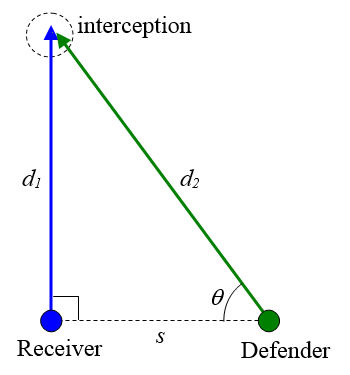
If the blue and green dots represent the initial positions of the players, the angle θ represents the running trajectory of the defender, and s is the initial distance between the two players, then the speed of the defender can be determined in order to intercept the receiver. Assume the two players are running at constant speed, and the speed of the receiver is V. From the geometry of the situation, d2sinθ = d1. Set T to be the travel time of both players before interception occurs. Divide both sides of the previous equation by T. The result is: d2sinθ/T = d1/T. Since d1/T = V, then this equation becomes d2sinθ/T = V. Divide both sides of this equation by sinθ, and the result is: d2/T = V/sinθ. The left side of this equation (d2/T) represents the speed of the defender, which is equal to V/sinθ. Note that the angle θ is arbitrary. The faster the defender can run relative to the receiver, the lower θ can be.
Air Resistance
The effect of air resistance is relevant during kicking and throwing, in which the distance the football travels is affected. Air resistance is another term for the drag force that the air exerts on an object during flight. Air resistance serves to slow the football down during flight, which decreases kicking or throwing distance, as shown in the figure below. If the long axis of the football is aligned with the trajectory path of the ball, then the frontal area of the football that is exposed to air drag is minimized, and the football flies further than, say, if the long side of the football was exposed to the air drag instead. In the figure below, vo is the initial launch velocity of the football, and θo is the initial launch angle.
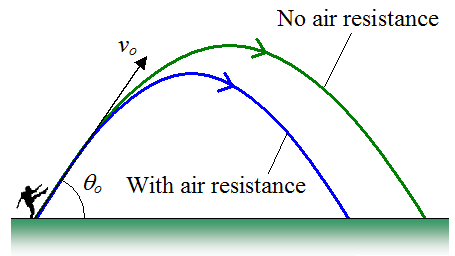
According to a paper by Ryan D. Hartschuh, Physics of Punting a Football, Physics Department, The College of Wooster, Wooster, Ohio (2002), the presence of air resistance decreases punting distance by 24-33% (relative to the theoretical punting distance that would occur in the absence of air resistance). However, air resistance has a nearly negligible effect on the amount of time that the football is airborne, and a good estimate of this so-called "hang time" can be calculated from the equations for projectile motion, which ignore the effect of air resistance. In this paper, the author mentions the "kicker's dilemma", in which the kicker must try to maximize both the punting distance and the hang time of the football. The kicker tries to maximize hang time to allow enough time for his teammates to run down field, and also tries to maximize punting distance to help his team’s field position. However, both these goals are in conflict with each other since maximum hang time occurs at a high launch angle of θo close to 90°, and punting distance is maximized at a launch angle of θo less than 45°. This assumes that the initial launch velocity vo of the football is kept constant.
Collision Between Players
When one player attempts to tackle another player, a force is exerted on each player, and on each player the force vector is equal and opposite to the force vector acting on the other player (Newton's third law). The figure below illustrates a general situation in which one player collides with another player. Body A can be thought of as the player doing the tackling, and body B can be thought of as the player carrying the ball. During the collision, the force vector FBA acts on body A, and this is equal and opposite to the force vector FAB which acts on body B. These forces act at the effective contact point C between the two players, during the collision. Based on a book by Timothy Gay, a professor of physics at the University of Nebraska-Lincoln: The Physics of Football, the center of mass (point G) and the effective pivot point (PA) of body A are both at the best position when they lie on the line of action of the impact force FBA, where the line of action is represented by the dashed line. When body A (the linebacker) is pushing on body B before body A establishes firm contact with the ground (at pivot PA), then having point G (on body A) lie on the line of action of FBA will ensure that there is no torque on body A (as a result, body A does not rotate). Once body A establishes firm contact with the ground, and the line of action of FBA passes through the effective pivot point PA of body A, then body A will not rotate because there is no torque to do so. However, the ball carrier (body B) will have a torque exerted on him due to the force FAB which creates a torque about his effective pivot point (PB) with the ground. This will cause body B to rotate and possibly fall over. (Note that the effective pivot point PA is the contact point between the linebacker’s back foot and the ground). This analysis is a result of assuming both bodies behave as rigid bodies, and experience a simplified case of two-dimensional (planar) motion.
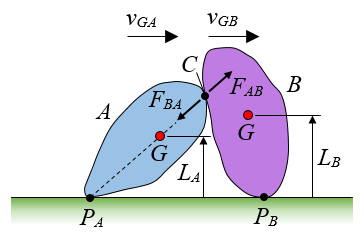
If the center of mass of body A is closer to the ground than body B (LA < LB), then body A is inherently more stable than body B (since body A is closer to the ground). A lower LA for body A means that, in general, there is a shorter moment (torque) arm (perpendicular distance between FBA and PA) than if body A were standing up straight. This means that it is harder to rotate body A. Consequently, it is easier to rotate body B (and cause him to fall over) than body A.
The collision between both bodies can also be analyzed using the conservation of momentum, assuming a simplified case of one-dimensional motion, and negligible ground (external) forces acting on the players during impact. Suppose vGA is the velocity of the center of mass of body A immediately before impact, and vGB is the velocity of the center of mass of body B immediately before impact. Then, mAvGA + mBvGB = (mA + mB)V, where mA is the mass of body A, mB is the mass of body B, and V is the velocity of the center of mass of both players immediately after impact (in which they move as a single object). From this equation we can solve for V = (mAvGA + mBvGB)/(mA + mB).
Football Bounce
When a football bounces, its motion is much more unpredictable than the bounce of a regular ball. The reason is because of the shape of a football, which results in contact forces with the ground having a largely variable line of action. Rod Cross, a physicist and retired academic of the University of Sydney, has written extensively on this subject. I base the following brief analysis on a paper that he wrote: Bounce of an oval shaped football.
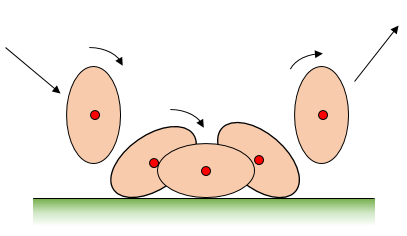
The shape of a football can be well approximated as a mathematical shape defined by a prolate spheroid. The bounce of a football is inherently a three-dimensional motion, but for the sake of simplicity, an analysis can be done for bounces that occur strictly in two-dimensions (planar motion). The following figure shows a football bouncing in two dimensions, with the different bounce stages shown; showing the football just before the bounce, during the bounce, and just after the bounce. Note that during the bounce the football makes contact with the ground, and rotates a bit, such that its orientation changes. During this rotation, the football can slide on the ground, roll (without slipping), or undergo a combination of both. The red dot represents the center of mass of the football.
During the impact stage, when the football makes contact with the ground, a basic two-dimensional analysis can be performed using the equations for impulse and momentum. To start off, consider the figure below showing a free-body diagram of the football as it makes contact with the ground, with sign convention as shown.
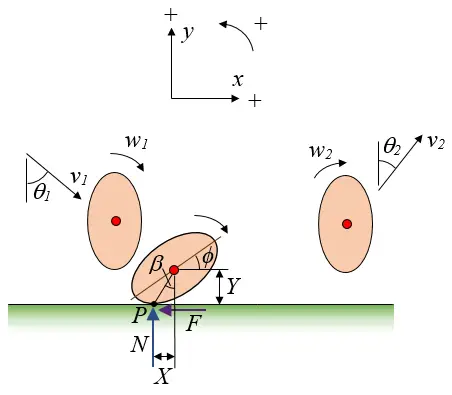
Where:
v1 is the velocity of the center of mass of the football immediately before impact
v2 is the velocity of the center of mass of the football immediately after impact
θ1 is the angle of the velocity vector of the center of mass of the football, with the vertical, immediately before impact
θ2 is the angle of the velocity vector of the center of mass of the football, with the vertical, immediately after impact
w1 is the angular velocity of the football immediately before impact
w2 is the angular velocity of the football immediately after impact
ϕ is the angle between the long axis of the football and the horizontal (during the impact)
P is the effective contact point between the football and ground (during the impact)
β is the angle between the vertical and the line joining the center of mass to point P (during the impact)
X is the horizontal distance between the center of mass and point P (during the impact)
Y is the vertical distance between the center of mass and point P (during the impact)
F is the horizontal contact force between the football and ground, at point P (during the impact)
N is the vertical contact force between the football and ground, at point P (during the impact)
Furthermore, let's introduce six new variables (not shown in the figure) which will be used shortly:
v1x is the velocity of the center of mass of the football in the x-direction immediately before impact
v2x is the velocity of the center of mass of the football in the x-direction immediately after impact
v1y is the velocity of the center of mass of the football in the y-direction immediately before impact
v2y is the velocity of the center of mass of the football in the y-direction immediately after impact
M is the mass of the football
IG is the moment of inertia of the football about the center of mass G
The equation for impulse and momentum in the x-direction is:
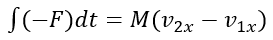
This simplifies to:
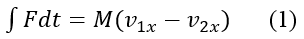
The equation for impulse and momentum in the y-direction is:
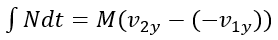
This simplifies to:
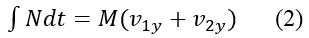
In equation (2), we reasonably assume that the vertical impulse contribution due to the weight of the football is negligible, as compared to the vertical impulse due to the force N. This is why the weight of the football is not included in equation (2).
For planar rotational motion, the equation for impulse and momentum is:
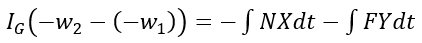
This simplifies to:
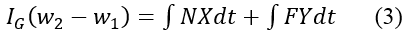
Equations (1)-(3) cannot be solved without having more information, such as determining whether or not the football slides or rolls on the ground, or does both. And this in turn is related to the coefficient of friction between the football and ground. In addition, the coefficient of restitution between football and ground also needs to be known. However, as it stands, equations (1)-(3) cover the basic physics of the impact between football and ground, and are illustrative in that regard.
Given certain values of football parameters, a football can bounce in interesting, yet unpredictable ways. It can even bounce backwards! This would mean that θ2 is between 270° and 360° (measured clockwise from the vertical, as indicated in the above figure). Such interesting manners of bouncing are well discussed by Rod Cross in his paper. If you wish to read more on the dynamics of the football bounce you can read his paper: Bounce of an oval shaped football.
Lastly, there is a myth in which it is debated on whether or not a football filled with helium can fly further than a regular football filled with air. The physics analysis of this myth is available here.
Football Flight
It is often the case that when a football is kicked or thrown, it undergoes an orientation change, when airborne, in which its long axis closely aligns with the flight path as it flies through the air. This orientation change is due to the effects of airflow over the football during flight. This orientation change happens when the football is given sufficient initial spin about its long axis. This creates gyroscopic stability which enables the football to keep its symmetric (long) axis aligned with its flight trajectory, without tumbling end over end when in flight. The spin imparts a gyroscopic response to the aerodynamic forces acting on the football, which results in the football long axis closely aligning itself with the flight trajectory (as shown below). The physics necessary to describe this is a combination of gyroscopic analysis and aerodynamic force analysis due to drag and (potentially) the Magnus effect. This is quite complicated and will not be discussed in detail here. However, there is a lot of literature available online on gyroscope physics, as related to projectile spin and gyroscopic stability, if one wishes to study this topic further.

The reason the long axis of the football follows the flight path is because of the gyroscopic effect. When the football is kicked or thrown, it is given an initial spin along its long axis. Let's call this spin rate ws. Once the football is released and is airborne, it immediately reacts to the air flow past its surface, and this results in a secondary spin, referred to as precession. Let's call this precession rate wp. It is this precession that gives the football the appearance of "wobbling" during flight. The figure below illustrates the spin and precession of a football.

As the football flies through the air, the trajectory of its center of mass follows a curved path. In order to keep air resistance as low as possible, and maximize distance, it is desirable that the long axis of the football follows this path (as described previously). The force of the air (drag force) acting on the football serves to rotate the football such that the long axis closely aligns with the flight path. Consider the figure below which shows the football moving at an arbitrary velocity V during its flight through the air. The resultant air drag force (represented by the dashed arrow) is directly opposite the direction of V. If the long axis of the football is oriented at an angle α relative to the direction of the air drag, as shown, then the air drag force has a moment arm relative to the center of mass G of the football, and as a result the air drag force exerts a torque on the football (represented by the green arrow). This torque tends to increase α. However, α does not increase continuously, as one might expect. Instead, the long axis of the football follows closely with the flight path, due to a gyroscopic effect. When this occurs, the football precesses about an axis closely aligned with the line of the flight path, and this line is continuously changing direction, which means that the precession axis changes too. It can then be said that the long axis of the football closely follows the flight path. This means that the precession axis (which is in the direction of vector wp) is kept closely aligned with the flight path at any point in time. Keep in mind that this is an ideal circumstance, however, and football flight can sometimes deviate from this scenario.

Now, if this same football were launched in a vacuum (with no air present), with the same initial spin about its long axis, it would not change orientation at all, and instead it would maintain its orientation throughout its flight. The figure below illustrates this.

The reason the football doesn't change its orientation is because there is only the force of gravity which exerts no torque on the football since it effectively acts through the center of mass of the football.
For more detail on the physics behind the flight of a football see:
P. J. Brancazio, Why does a football keep its axis pointing along its trajectory?, The Physics Teacher, 23, 571-573 (1985).
C. Horn and H. Fearn, On the Flight of the American Football, Physics Department, California State University Fullerton (2007).
Interception
The diagram below shows a common situation in which a defender needs to intercept a receiver. In this situation, the travel path of the player doing the intercepting (the defender) must intersect the travel path of the receiver. The blue arrow represents the path of the receiver, and the green arrow represents the path of the defender.

If the blue and green dots represent the initial positions of the players, the angle θ represents the running trajectory of the defender, and s is the initial distance between the two players, then the speed of the defender can be determined in order to intercept the receiver. Assume the two players are running at constant speed, and the speed of the receiver is V. From the geometry of the situation, d2sinθ = d1. Set T to be the travel time of both players before interception occurs. Divide both sides of the previous equation by T. The result is: d2sinθ/T = d1/T. Since d1/T = V, then this equation becomes d2sinθ/T = V. Divide both sides of this equation by sinθ, and the result is: d2/T = V/sinθ. The left side of this equation (d2/T) represents the speed of the defender, which is equal to V/sinθ. Note that the angle θ is arbitrary. The faster the defender can run relative to the receiver, the lower θ can be.
Air Resistance
The effect of air resistance is relevant during kicking and throwing, in which the distance the football travels is affected. Air resistance is another term for the drag force that the air exerts on an object during flight. Air resistance serves to slow the football down during flight, which decreases kicking or throwing distance, as shown in the figure below. If the long axis of the football is aligned with the trajectory path of the ball, then the frontal area of the football that is exposed to air drag is minimized, and the football flies further than, say, if the long side of the football was exposed to the air drag instead. In the figure below, vo is the initial launch velocity of the football, and θo is the initial launch angle.

According to a paper by Ryan D. Hartschuh, Physics of Punting a Football, Physics Department, The College of Wooster, Wooster, Ohio (2002), the presence of air resistance decreases punting distance by 24-33% (relative to the theoretical punting distance that would occur in the absence of air resistance). However, air resistance has a nearly negligible effect on the amount of time that the football is airborne, and a good estimate of this so-called "hang time" can be calculated from the equations for projectile motion, which ignore the effect of air resistance. In this paper, the author mentions the "kicker's dilemma", in which the kicker must try to maximize both the punting distance and the hang time of the football. The kicker tries to maximize hang time to allow enough time for his teammates to run down field, and also tries to maximize punting distance to help his team’s field position. However, both these goals are in conflict with each other since maximum hang time occurs at a high launch angle of θo close to 90°, and punting distance is maximized at a launch angle of θo less than 45°. This assumes that the initial launch velocity vo of the football is kept constant.
Collision Between Players
When one player attempts to tackle another player, a force is exerted on each player, and on each player the force vector is equal and opposite to the force vector acting on the other player (Newton's third law). The figure below illustrates a general situation in which one player collides with another player. Body A can be thought of as the player doing the tackling, and body B can be thought of as the player carrying the ball. During the collision, the force vector FBA acts on body A, and this is equal and opposite to the force vector FAB which acts on body B. These forces act at the effective contact point C between the two players, during the collision. Based on a book by Timothy Gay, a professor of physics at the University of Nebraska-Lincoln: The Physics of Football, the center of mass (point G) and the effective pivot point (PA) of body A are both at the best position when they lie on the line of action of the impact force FBA, where the line of action is represented by the dashed line. When body A (the linebacker) is pushing on body B before body A establishes firm contact with the ground (at pivot PA), then having point G (on body A) lie on the line of action of FBA will ensure that there is no torque on body A (as a result, body A does not rotate). Once body A establishes firm contact with the ground, and the line of action of FBA passes through the effective pivot point PA of body A, then body A will not rotate because there is no torque to do so. However, the ball carrier (body B) will have a torque exerted on him due to the force FAB which creates a torque about his effective pivot point (PB) with the ground. This will cause body B to rotate and possibly fall over. (Note that the effective pivot point PA is the contact point between the linebacker’s back foot and the ground). This analysis is a result of assuming both bodies behave as rigid bodies, and experience a simplified case of two-dimensional (planar) motion.

If the center of mass of body A is closer to the ground than body B (LA < LB), then body A is inherently more stable than body B (since body A is closer to the ground). A lower LA for body A means that, in general, there is a shorter moment (torque) arm (perpendicular distance between FBA and PA) than if body A were standing up straight. This means that it is harder to rotate body A. Consequently, it is easier to rotate body B (and cause him to fall over) than body A.
The collision between both bodies can also be analyzed using the conservation of momentum, assuming a simplified case of one-dimensional motion, and negligible ground (external) forces acting on the players during impact. Suppose vGA is the velocity of the center of mass of body A immediately before impact, and vGB is the velocity of the center of mass of body B immediately before impact. Then, mAvGA + mBvGB = (mA + mB)V, where mA is the mass of body A, mB is the mass of body B, and V is the velocity of the center of mass of both players immediately after impact (in which they move as a single object). From this equation we can solve for V = (mAvGA + mBvGB)/(mA + mB).
Football Bounce
When a football bounces, its motion is much more unpredictable than the bounce of a regular ball. The reason is because of the shape of a football, which results in contact forces with the ground having a largely variable line of action. Rod Cross, a physicist and retired academic of the University of Sydney, has written extensively on this subject. I base the following brief analysis on a paper that he wrote: Bounce of an oval shaped football.
The shape of a football can be well approximated as a mathematical shape defined by a prolate spheroid. The bounce of a football is inherently a three-dimensional motion, but for the sake of simplicity, an analysis can be done for bounces that occur strictly in two-dimensions (planar motion). The following figure shows a football bouncing in two dimensions, with the different bounce stages shown; showing the football just before the bounce, during the bounce, and just after the bounce. Note that during the bounce the football makes contact with the ground, and rotates a bit, such that its orientation changes. During this rotation, the football can slide on the ground, roll (without slipping), or undergo a combination of both. The red dot represents the center of mass of the football.

During the impact stage, when the football makes contact with the ground, a basic two-dimensional analysis can be performed using the equations for impulse and momentum. To start off, consider the figure below showing a free-body diagram of the football as it makes contact with the ground, with sign convention as shown.

Where:
v1 is the velocity of the center of mass of the football immediately before impact
v2 is the velocity of the center of mass of the football immediately after impact
θ1 is the angle of the velocity vector of the center of mass of the football, with the vertical, immediately before impact
θ2 is the angle of the velocity vector of the center of mass of the football, with the vertical, immediately after impact
w1 is the angular velocity of the football immediately before impact
w2 is the angular velocity of the football immediately after impact
ϕ is the angle between the long axis of the football and the horizontal (during the impact)
P is the effective contact point between the football and ground (during the impact)
β is the angle between the vertical and the line joining the center of mass to point P (during the impact)
X is the horizontal distance between the center of mass and point P (during the impact)
Y is the vertical distance between the center of mass and point P (during the impact)
F is the horizontal contact force between the football and ground, at point P (during the impact)
N is the vertical contact force between the football and ground, at point P (during the impact)
Furthermore, let's introduce six new variables (not shown in the figure) which will be used shortly:
v1x is the velocity of the center of mass of the football in the x-direction immediately before impact
v2x is the velocity of the center of mass of the football in the x-direction immediately after impact
v1y is the velocity of the center of mass of the football in the y-direction immediately before impact
v2y is the velocity of the center of mass of the football in the y-direction immediately after impact
M is the mass of the football
IG is the moment of inertia of the football about the center of mass G
The equation for impulse and momentum in the x-direction is:
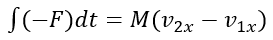
This simplifies to:
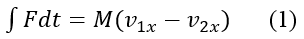
The equation for impulse and momentum in the y-direction is:
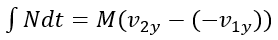
This simplifies to:
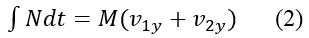
In equation (2), we reasonably assume that the vertical impulse contribution due to the weight of the football is negligible, as compared to the vertical impulse due to the force N. This is why the weight of the football is not included in equation (2).
For planar rotational motion, the equation for impulse and momentum is:
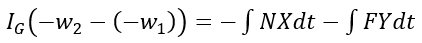
This simplifies to:
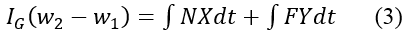
Equations (1)-(3) cannot be solved without having more information, such as determining whether or not the football slides or rolls on the ground, or does both. And this in turn is related to the coefficient of friction between the football and ground. In addition, the coefficient of restitution between football and ground also needs to be known. However, as it stands, equations (1)-(3) cover the basic physics of the impact between football and ground, and are illustrative in that regard.
Given certain values of football parameters, a football can bounce in interesting, yet unpredictable ways. It can even bounce backwards! This would mean that θ2 is between 270° and 360° (measured clockwise from the vertical, as indicated in the above figure). Such interesting manners of bouncing are well discussed by Rod Cross in his paper. If you wish to read more on the dynamics of the football bounce you can read his paper: Bounce of an oval shaped football.
Lastly, there is a myth in which it is debated on whether or not a football filled with helium can fly further than a regular football filled with air. The physics analysis of this myth is available here.


Post a Comment